|
|
|
 |
 |
AEO-2Using the rule method, the middle term is distributed in the minor premise (2nd premise). The major term (P) is distributed in the conclusion, but is also distributed in its premise. A negative conclusion exists for the negative premise and a negative premise exists for the negative conclusion. There are not two negative premises. So all rules are passed. Thus the argument is valid.All P are M
No S are M
Some S are not P
Warning: Web Page Notes are not intended as a substitute for attending lectures.
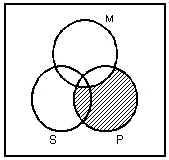
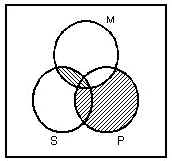
Using the Venn Diagram method
will produce the following diagram:
|
|
|
 |
 |
Since the conclusion requires that an asterisk occur
in the part of the S circle outside the P circle and there is no asterisk
at all in the diagram the argument is invalid! How can this be?
First, you should know that you need not worry since, for the purposes of the Wiebster's Philosophy class you will always be told which method to use. Second, the reason for the disagreement is that the two methods make different assumptions about the existence of members in the subject class (the subject term of propositions). The Venn Diagram method does not assume that any members of the subject class of universal propositions exist. Thus diagrams for universal propositions do not include an asterisk. But traditional logic, on which our rules are based, did assume that members of the subject class did exist. So, as long as you are arguing about things that actually do exist, the rule method will work just fine. You can trust its results. But if you are discussing things that do not exist, then you should use the Venn Diagram method. The Venn Diagram method will never indicate that an argument is valid when it is not, but it may sometimes indicate that an argument is invalid when, given that it was about things that exist, the conclusion could not be false if the premises are true.